二分法
-
折半查找又称二分查找,仅适用于有序的顺序表 (可随机访问,链表不行)。
-
给出如下形式的代码:假设查找表为从小到大的有序表,显然一般而言当 时认为查找失败。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28typedef int ElemType;
typedef struct
{
ElemType *elem;
int tableLen;
} SSTable;
int Binary_Search(SSTable L, ElemType key)
{
int low = 0, high = L.tableLen - 1, mid;
while (low <= high)
{
mid = (low + high) / 2;
if (L.elem[mid] == key)
{
return mid;
}
else if (L.elem[mid] > key) // key在左半区
{
high = mid - 1;
}
else // key在右半区
{
low = mid + 1;
}
}
return -1;
} -
折半查找判定树构成:首先我们要知道在 c 或 c++语言中, 其实是等同于 。
- 时:每次二分后,到元素个数的奇偶性是可能发生变化的。
- 若 到 共有奇数个元素时,则 分隔后,左右两边元素个数相等。
- 若 到 共有偶数个元素时,则 分隔后,左边元素个数比右边少一个。
- 对于任意一个判定树结点,右子树结点数-左子树结点数= 或者 。
- 时:
- 若 到 共有奇数个元素时,则 分隔后,左右两边元素个数相等。
- 若 到 共有偶数个元素时,则 分隔后,右边元素个数比左边少一个。
- 对于任意一个判定树结点,左子树结点数-右子树结点数= 或者 。
- 故而经上面分析,折半查找的判定树一定是平衡二叉树,且除最后一层可能不满以外,其它层都是满的。含有元素个数的树高 (不含失败结点) 为,显然且,即折半查找时间复杂度。但是请注意,这不意味着任何情况下折半查找的效率均高于顺序查找,例如查找查找表的第一个元素。
- 显然依旧满足:若有个结点,则相应地有个查找失败结点 (成功结点的空链域数量)。
- 下面我们不妨演示一下 的判定树构建过程 (下图省略失败结点部分):
- 显然按照左子树比右子树少一原则, 和 因该是右孩子。
- 当然我们其实要知道在折半查找的判定树中,左右子树其实就是在折半过程中划分的左右区间。当 时显然 属于右区间内,故而在右子树中, 同理可得。
- 不妨判断一下面的二叉树是否可能是折半查找的判定树:显然不是,不可能一会右子树比左子树多,一会儿左子树比右子树多。
- 时:每次二分后,到元素个数的奇偶性是可能发生变化的。
-
提醒一点:
mid=(left+right)/2存在left+right过大导致溢出的风险,推荐使用mid=left+(right-left)/2。 -
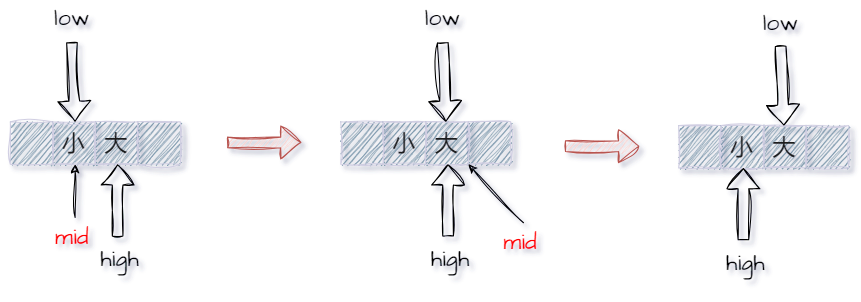
为了后续分块查找部分,提一嘴。实际上查找关键字并不是二分查找的全部内容,例如如何找到一个比关键字大的最小值、或者找比关键字小的最大值。实际上我们要知道一点:查找失败,和会分别指向比目标值稍大和稍小的元素,如下图两种情况的演示。当然也可以直接尝试逻辑分析,当时,若显然右移,反之左移,故而不难看出上述结论。不妨尝试力扣题:搜索插入位置 (由于不存在重复,若找到相等元素时返回当前位置即可)
-
补充:但是对于上述问题,其存在一个前提查找表中无重复元素。但是当我们允许重复时情况似乎略复杂,即允许存在重复元素,此时我们需要深入理解一下二分法的原理:为了方便叙述,这里暂时使用 代替 ,开启上帝视角,将程序的查找结果(最终返回值)记作 。
-
前提:关于程序结束条件的讨论
-
low<high:当循环结束时low=high,此时对于双闭区间()而言,我们已经找到一个值,下一步就是判断是不是我们要的,不是则没结果。 -
low<=high:当循环结束时low=high+1,此时对于双闭区间()而言,我们找到两个值high和low。这时后我们需要判断,我们是其中哪一个,还是都不是。 -
实际上
low<=high就是在low<high的基础上再运行了一遍程序,这个过程其实就可以认为将low=high得到的唯一结果进行验算,判断是否为我们要的。
-
-
现在,我们不妨提出以下两个问题:
- :在一个存在重复元素的查找表中,我们需要找到比大的最小值。
- :在一个存在重复元素的查找表中,我们需要找到比小的最大值。
-
显然无论是哪个问题,有一点我们需要肯定。当
low=high时,我们就要终止程序,即终止条件仍为low<high(这一点通过后面讨论很容易理解)。而一般二分法之所以在low=high后还执行一遍程序,是为了判断最终找到位置的关键字是不是key。参照这个形式,其实可以写出另一种二分法代码如下,这个我们后面再说。 -
对于问题 ,当我们发现 时,我们该怎么做?显然我们需要找比 大的,我们可以直接 。当我们发现 时,我们该怎么做?显然我们需要保留 ,因为 可能就是我们需要的结果,即 。给出下列代码:
1
2
3
4
5
6
7
8
9
10
11
12
13int binary_search(SSTable ST, ElemType key)
{
int low = 0, high = ST.tableLen - 1, mid;
while (low < high)
{
mid = (low + high) / 2;
if (ST.elem[mid] <= key)
low = mid + 1;
else
high = mid;
}
return ST.elem[low] > key ? low : -1;
} -
当然对于上述代码最后返回值可能存在一些小的疑问,为啥不直接返回
low?其实可能high一直没动,low一路狂奔追上high,也就是说整个数组可能不存在比key大的数。 -
那么若将
low<high的条件换为low>=high呢?给出如下代码:显然当high=low时,我们找到可能结果; 此时若low是所求ans则low不变,否则low加一则没找则返回low即可(当然也可以推测low+1=high时的情形)。1
2
3
4
5
6
7
8
9
10
11
12
13int Search_Bin(SSTable ST, ElemType key)
{
int low = 0, high = ST.tableLen - 1, mid;
while (low <= high)
{
mid = (low + high) / 2;
if (ST.elem[mid] <= key)
low = mid + 1;
else
high = mid;
}
return low; // high+1也是可以的
} -
同样的,对于问题 , 当我们发现 时,我们该怎么做?显然我们需要找比 小的,我们可以直接 。当我们发现 时,我们该怎么做?显然我们需要保留 ,因为 可能就是我们需要的结果,即 。给出下列代码:
1
2
3
4
5
6
7
8
9
10
11
12
13int Search_Bin(SSTable ST, ElemType key)
{
int low = 0, high = ST.tableLen - 1, mid;
while (low < high)
{
mid = (low + high) / 2;
if (ST.elem[mid] < key)
low = mid;
else
high = mid - 1;
}
return ST.elem[high] < key ? high : -1;
} -
同理可以写出问题的另一种代码:
1
2
3
4
5
6
7
8
9
10
11
12
13int Search_Bin(SSTable ST, ElemType key)
{
int low = 0, high = ST.tableLen - 1, mid;
while (low <= high)
{
mid = (low + high) / 2;
if (ST.elem[mid] < key)
low = mid;
else
high = mid - 1;
}
return high; // low-1也是可以的
} -
实际上,我们给出折半查找的另一种解释,即排除法解释,上述代码就会变得和蔼可亲。
-
先以基本的折半查找为例,当我们发现 ,显然我们的 于是乎排除右区间转向左区间,其代码语言就是 。而当我们发现 ,显然我们的 于是乎排除左区间转向右区间,其代码语言就是 。
-
在次回到 问题中,我们的 ,当 , 显然我们显然需要排除左区间,同理当 ,我们也需要丢弃左区间,转换为代码语言就是 。那么当 时,此时 可能就是 ,需要保留 。对于 问题同理分析即可。
-
排除法的精髓在于,不断排除不可能存在结果的区间直至区间长度为1,那么我们的结果要不就是这玩意,要不就没结果。于是我们根据上述知识得到新的二分代码:当然不难看出,这种形式的效率较低,每次都需要遍历整个表才能得出最后结果,哪怕是中间某个过程中。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17int Binary_Search(SSTable L, ElemType key)
{
int low = 0, high = L.tableLen - 1, mid;
while (low < high)
{
mid = (low + high) / 2;
if (L.elem[mid] > key)
{
high = mid - 1;
}
else
{
low = mid;
}
}
return L.elem[low] == key ? low : low - 1;
}1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18int Binary_Search(SSTable L, ElemType key)
{
int low = 0, high = L.tableLen - 1, mid;
while (low < high)
{
mid = (low + high) / 2;
if (L.elem[mid] < key)
{
low = mid + 1;
}
else
{
high = mid;
}
}
return L.elem[low] == key ? low : low - 1;
}
-
-
此外对于 和 问题,我们提出另一种略难理解的方式,区间开闭。
-
给出示意图:其中数组长度为
-
对于 问题,我们需要找比 大的关键字,即 。那么 在数组中的位置在哪儿?显然存在多种表示:
-
,我们称这种为双闭区间,就是我们上面代码所使用的区间法。
-
,我们称这种为左闭右开区间,这种形式可以解决问题:我们在理论上
n补上,这样就没有必要在high=low后验证一次,也不能验证,验证就可能导致数组越界。1
2
3
4
5
6
7
8
9
10
11
12
13int binary_search(SSTable ST, ElemType key)
{
int low = 0, high = ST.tableLen, mid;
while (low < high)
{
mid = (low + high) / 2;
if (ST.elem[mid] <= key)
low = mid + 1;
else
high = mid;
}
return low;
} -
,我们称这种为左开右闭区间,这种形式可以解决问题:原理同上。
1
2
3
4
5
6
7
8
9
10
11
12
13int Search_Bin(SSTable ST, ElemType key)
{
int low = -1, high = ST.tableLen - 1, mid;
while (low < high)
{
mid = (low + high) / 2;
if (ST.elem[mid] < key)
low = mid;
else
high = mid - 1;
}
return high;
}
-
-
-
指鹿为马:实际上,我们前面在二分法(不含有重复元素)中提过:查找失败,和会分别指向比目标值稍大和稍小的元素。那对于问题,我们倘若将执行的操作归类到的操作(将所有的视作),那么最终就演变成了最开始不含重复元素且必然查找失败的情景。那对于问题同理(将所有的视作)
-
对于问题:
1
2
3
4
5
6
7
8
9
10
11
12
13int Search_Bin(SSTable ST, ElemType key)
{
int low = 0, high = ST.tableLen, mid; // 左闭右开
while (low <= high)
{
mid = (low + high) / 2;
if (ST.elem[mid] <= key)
low = mid + 1;
else
high = mid - 1;
}
return low;
} -
对于问题:
1
2
3
4
5
6
7
8
9
10
11
12
13int Search_Bin(SSTable ST, ElemType key)
{
int low = -1, high = ST.tableLen-1, mid; // 左开右闭
while (low <= high)
{
mid = (low + high) / 2;
if (ST.elem[mid] >= key)
high = mid - 1;
else
low = mid + 1;
}
return high;
}
-
-
-
最终给出一个图和一句话:二分法的关键还是讨论
low=high以及其前、后一步的执行情况。